Contoh Besaran Pokok dan Besaran Turunan Panduan Lengkap dan Mudah Dipahami

Memahami dunia fisika dimulai dengan penguasaan konsep dasar, dan salah satunya adalah tentang contoh besaran pokok dan besaran turunan. Kedua jenis besaran ini adalah fondasi penting yang memungkinkan untuk mengukur, menganalisis, dan memahami fenomena alam di sekitar.

Besaran pokok adalah entitas dasar yang berdiri sendiri dan tidak bergantung pada besaran lain, seperti panjang, massa, waktu, suhu, kuat arus listrik, intensitas cahaya, dan jumlah zat. Sementara itu, besaran turunan adalah hasil kombinasi dari besaran pokok, misalnya kecepatan, luas, volume, gaya, dan energi. Konsep ini krusial dalam berbagai bidang, mulai dari ilmu pengetahuan hingga teknologi, dan bahkan dalam kehidupan sehari-hari.

Pengantar: Memahami Besaran Pokok dan Turunan

Dalam dunia fisika, kita seringkali berhadapan dengan berbagai macam pengukuran dan perhitungan. Untuk memahami dunia fisik dengan lebih baik, kita perlu memahami dua kategori utama besaran: besaran pokok dan besaran turunan. Kedua jenis besaran ini adalah fondasi penting dalam ilmu fisika, memungkinkan kita untuk mendeskripsikan dan memprediksi fenomena alam.

Perbedaan mendasar antara besaran pokok dan turunan terletak pada cara mereka didefinisikan dan diukur. Besaran pokok adalah besaran yang didefinisikan secara independen dan menjadi dasar untuk besaran lainnya. Sementara itu, besaran turunan adalah besaran yang diturunkan dari kombinasi besaran pokok.

Perbedaan Mendasar Besaran Pokok dan Turunan

Perbedaan utama antara besaran pokok dan turunan terletak pada definisi dan asal-usulnya. Besaran pokok berdiri sendiri dan tidak bergantung pada besaran lain untuk didefinisikan. Sebaliknya, besaran turunan dibangun dari kombinasi besaran pokok.

Besaran Pokok: Besaran ini bersifat fundamental dan tidak dapat didefinisikan dari besaran lain. Mereka berfungsi sebagai dasar pengukuran dalam sistem satuan. Contohnya adalah panjang, massa, waktu, suhu, kuat arus listrik, intensitas cahaya, dan jumlah zat.
Besaran Turunan: Besaran ini didefinisikan dari kombinasi dua atau lebih besaran pokok melalui operasi matematika seperti perkalian, pembagian, atau perpangkatan. Contohnya adalah luas, volume, kecepatan, percepatan, gaya, energi, dan daya.

Contoh Besaran Pokok dan Pengukurannya

Besaran pokok memiliki peran krusial dalam pengukuran. Mereka adalah dasar dari sistem pengukuran yang kita gunakan sehari-hari. Berikut adalah beberapa contoh besaran pokok dan cara pengukurannya:

Panjang: Diukur dalam satuan meter (m). Pengukuran panjang dapat dilakukan menggunakan penggaris, meteran, atau alat ukur lainnya.
Massa: Diukur dalam satuan kilogram (kg). Massa diukur menggunakan timbangan, baik timbangan digital maupun timbangan neraca.
Waktu: Diukur dalam satuan detik (s). Waktu diukur menggunakan jam, stopwatch, atau alat pengukur waktu lainnya.
Suhu: Diukur dalam satuan Kelvin (K), meskipun dalam kehidupan sehari-hari sering menggunakan Celcius (°C). Suhu diukur menggunakan termometer.
Kuat Arus Listrik: Diukur dalam satuan Ampere (A). Kuat arus listrik diukur menggunakan amperemeter.
Intensitas Cahaya: Diukur dalam satuan Candela (cd). Intensitas cahaya diukur menggunakan alat khusus yang disebut luxmeter.
Jumlah Zat: Diukur dalam satuan mol (mol). Jumlah zat diukur menggunakan konsep kimia dan perhitungan berdasarkan massa molar.

Contoh Besaran Turunan dan Penurunannya

Besaran turunan sangat penting dalam menggambarkan berbagai fenomena fisika. Mereka diturunkan dari kombinasi besaran pokok melalui operasi matematika. Berikut adalah beberapa contoh besaran turunan dan bagaimana mereka diturunkan:

Luas: Diturunkan dari besaran pokok panjang. Luas (A) suatu bidang datar dihitung dengan mengalikan panjang (l) dan lebar (w):

A = l × w

Satuan luas adalah meter persegi (m²).
Volume: Diturunkan dari besaran pokok panjang. Volume (V) suatu benda tiga dimensi dihitung dengan mengalikan panjang (l), lebar (w), dan tinggi (h):

V = l × w × h

Satuan volume adalah meter kubik (m³).
Kecepatan: Diturunkan dari besaran pokok panjang dan waktu. Kecepatan (v) dihitung dengan membagi jarak (s) yang ditempuh dengan waktu (t):

v = s / t

Satuan kecepatan adalah meter per detik (m/s).
Percepatan: Diturunkan dari besaran pokok panjang dan waktu. Percepatan (a) dihitung dengan perubahan kecepatan (Δv) dibagi dengan perubahan waktu (Δt):

a = Δv / Δt

Satuan percepatan adalah meter per detik kuadrat (m/s²).
Gaya: Diturunkan dari besaran pokok massa, panjang, dan waktu. Gaya (F) dihitung menggunakan Hukum Newton kedua: massa (m) dikalikan dengan percepatan (a):

F = m × a

Satuan gaya adalah Newton (N).
Energi: Diturunkan dari besaran pokok massa, panjang, dan waktu. Energi (E) memiliki berbagai bentuk, salah satunya adalah energi kinetik yang dihitung sebagai:

E = 1/2 × m × v²

Satuan energi adalah Joule (J).
Daya: Diturunkan dari besaran pokok massa, panjang, dan waktu. Daya (P) dihitung sebagai energi (E) dibagi dengan waktu (t):

P = E / t

Satuan daya adalah Watt (W).

Pentingnya Pemahaman Konsep Besaran Pokok dan Turunan

Pemahaman yang kuat tentang besaran pokok dan turunan adalah fundamental dalam fisika. Konsep ini menyediakan kerangka kerja untuk memahami, menganalisis, dan memecahkan masalah dalam berbagai bidang fisika. Dengan memahami besaran-besaran ini, kita dapat merumuskan hukum-hukum fisika, memprediksi perilaku sistem fisik, dan mengembangkan teknologi baru. Tanpa pemahaman yang baik tentang besaran pokok dan turunan, studi fisika akan menjadi sangat sulit dan tidak efektif.

Ilustrasi Deskriptif Hubungan Besaran Pokok dan Turunan

Bayangkan sebuah pohon. Akar pohon adalah besaran pokok, yang menyediakan fondasi yang kokoh. Batang pohon adalah representasi dari cara besaran pokok ini berinteraksi. Cabang-cabang pohon adalah besaran turunan, yang muncul dari kombinasi akar dan batang. Misalnya, akar (panjang, waktu) berinteraksi melalui batang (perkalian, pembagian) untuk menghasilkan cabang (kecepatan, percepatan).

Daun-daun pada cabang (energi, gaya) menggambarkan bagaimana besaran turunan ini digunakan untuk menggambarkan fenomena yang lebih kompleks. Pohon ini menggambarkan bagaimana besaran pokok menjadi dasar bagi besaran turunan, yang pada gilirannya memungkinkan kita memahami dunia fisik yang kompleks.

Besaran Pokok

Besaran pokok adalah dasar dari pengukuran dalam fisika. Mereka didefinisikan secara independen dan tidak bergantung pada besaran lain. Pemahaman yang jelas tentang besaran pokok sangat penting karena semua besaran turunan dibangun berdasarkan besaran-besaran ini. Artikel ini akan menguraikan definisi, satuan, alat ukur, dan bagaimana mereka berperan dalam perhitungan besaran turunan.

Definisi dan Satuan Besaran Pokok

Setiap besaran pokok memiliki definisi yang jelas dan satuan yang ditetapkan dalam Sistem Internasional (SI). Satuan SI memberikan standar yang konsisten untuk pengukuran di seluruh dunia. Berikut adalah daftar besaran pokok beserta definisi dan satuannya:

Panjang: Definisi: Jarak antara dua titik. Satuan SI: Meter (m).
Massa: Definisi: Jumlah materi yang terkandung dalam suatu benda. Satuan SI: Kilogram (kg).
Waktu: Definisi: Durasi antara dua kejadian. Satuan SI: Detik (s).
Arus Listrik: Definisi: Laju aliran muatan listrik. Satuan SI: Ampere (A).
Suhu Termodinamika: Definisi: Ukuran energi kinetik rata-rata partikel dalam suatu sistem. Satuan SI: Kelvin (K).
Jumlah Zat: Definisi: Ukuran jumlah entitas elementer (atom, molekul, ion, dll.) dalam suatu zat. Satuan SI: Mol (mol).
Intensitas Cahaya: Definisi: Daya pancar cahaya per satuan sudut padat. Satuan SI: Candela (cd).

Alat Ukur Besaran Pokok, Contoh besaran pokok dan besaran turunan

Setiap besaran pokok diukur menggunakan alat ukur yang spesifik. Pemilihan alat ukur yang tepat penting untuk mendapatkan hasil pengukuran yang akurat.

Panjang: Alat ukur: Mistar, jangka sorong, mikrometer sekrup.
Massa: Alat ukur: Timbangan, neraca.
Waktu: Alat ukur: Jam, stopwatch.
Arus Listrik: Alat ukur: Amperemeter.
Suhu Termodinamika: Alat ukur: Termometer.
Jumlah Zat: Alat ukur: Tidak ada alat ukur langsung; dihitung berdasarkan pengukuran massa dan massa molar.
Intensitas Cahaya: Alat ukur: Luxmeter.

Penggunaan Satuan Besaran Pokok dalam Perhitungan Besaran Turunan

Besaran turunan didefinisikan sebagai besaran yang diturunkan dari satu atau lebih besaran pokok. Satuan besaran turunan diperoleh dari kombinasi satuan besaran pokok. Sebagai contoh:

Luas = Panjang x Lebar. Satuan: m x m = m²

Kecepatan = Jarak / Waktu. Satuan: m / s

Gaya = Massa x Percepatan. Satuan: kg x m/s ² (Newton, N)

Tabel Besaran Pokok

Tabel berikut merangkum besaran pokok, simbol, satuan SI, dan alat ukurnya:

Besaran Pokok	Simbol	Satuan SI	Alat Ukur
Panjang	l	Meter (m)	Mistar, Jangka Sorong, Mikrometer Sekrup
Massa	m	Kilogram (kg)	Timbangan, Neraca
Waktu	t	Detik (s)	Jam, Stopwatch
Arus Listrik	I	Ampere (A)	Amperemeter
Suhu Termodinamika	T	Kelvin (K)	Termometer
Jumlah Zat	n	Mol (mol)	Tidak ada alat ukur langsung
Intensitas Cahaya	I_v	Candela (cd)	Luxmeter

Pengaruh Kesalahan Pengukuran

Kesalahan dalam pengukuran besaran pokok akan mempengaruhi hasil perhitungan besaran turunan. Kesalahan ini dapat berasal dari berbagai sumber, seperti kesalahan kalibrasi alat ukur, kesalahan paralaks, atau kesalahan manusia. Contohnya:

Contoh 1: Mengukur panjang balok dengan mistar. Jika mistar tidak dikalibrasi dengan benar, atau pembacaan tidak tepat (kesalahan paralaks), maka luas balok (Panjang x Lebar) yang dihitung akan salah. Semakin besar kesalahan pada pengukuran panjang dan lebar, semakin besar pula kesalahan pada perhitungan luas.
Contoh 2: Mengukur waktu tempuh mobil. Jika stopwatch tidak berfungsi dengan baik atau waktu reaksi pengamat lambat, kecepatan mobil (Jarak / Waktu) yang dihitung akan tidak akurat.

Penting untuk memahami sumber kesalahan dan berusaha meminimalkannya untuk mendapatkan hasil perhitungan yang lebih akurat.

Besaran Turunan

Besaran turunan adalah besaran fisika yang didefinisikan dari kombinasi besaran pokok. Mereka tidak berdiri sendiri sebagai satuan dasar, melainkan diturunkan melalui operasi matematika tertentu yang melibatkan satu atau lebih besaran pokok. Pemahaman tentang besaran turunan sangat penting dalam berbagai bidang ilmu pengetahuan dan teknologi, karena mereka memungkinkan kita untuk mengukur dan memahami fenomena yang lebih kompleks.

Pembentukan Besaran Turunan dari Besaran Pokok

Besaran turunan dibentuk melalui operasi matematika seperti perkalian, pembagian, atau kombinasi dari keduanya, yang melibatkan besaran pokok. Misalnya, luas diturunkan dari panjang dan lebar (keduanya besaran pokok panjang), sedangkan kecepatan diturunkan dari jarak (panjang) dan waktu (besaran pokok waktu). Proses ini memungkinkan kita untuk mengukur dan menggambarkan konsep-konsep fisika yang lebih kompleks daripada hanya menggunakan besaran pokok secara terpisah.

Contoh Perhitungan Besaran Turunan

Berikut adalah beberapa contoh perhitungan besaran turunan dengan menggunakan rumus:

Luas (A): Luas adalah besaran turunan yang mengukur seberapa banyak permukaan yang tertutupi oleh suatu objek. Rumus untuk menghitung luas persegi panjang adalah panjang (p) dikalikan lebar (l): A = p × l. Jika sebuah persegi panjang memiliki panjang 5 meter dan lebar 3 meter, maka luasnya adalah A = 5 m × 3 m = 15 m².
Kecepatan (v): Kecepatan mengukur seberapa cepat suatu objek bergerak. Rumus untuk menghitung kecepatan adalah jarak (s) dibagi waktu (t): v = s / t. Jika sebuah mobil menempuh jarak 100 meter dalam waktu 10 detik, maka kecepatannya adalah v = 100 m / 10 s = 10 m/s.
Massa Jenis (ρ): Massa jenis mengukur seberapa banyak massa suatu zat terkandung dalam volume tertentu. Rumus untuk menghitung massa jenis adalah massa (m) dibagi volume (V): ρ = m / V. Jika sebuah balok memiliki massa 200 gram dan volume 100 cm³, maka massa jenisnya adalah ρ = 200 g / 100 cm³ = 2 g/cm³.

Satuan Besaran Turunan

Satuan besaran turunan diturunkan dari satuan besaran pokok yang membentuknya. Misalnya, satuan luas (m²) diturunkan dari satuan panjang (m), karena luas dihitung dengan mengalikan panjang dan lebar (keduanya dalam satuan meter). Satuan kecepatan (m/s) diturunkan dari satuan panjang (m) dan satuan waktu (s). Pemahaman tentang bagaimana satuan turunan diturunkan penting untuk memastikan konsistensi dan keakuratan dalam perhitungan fisika.

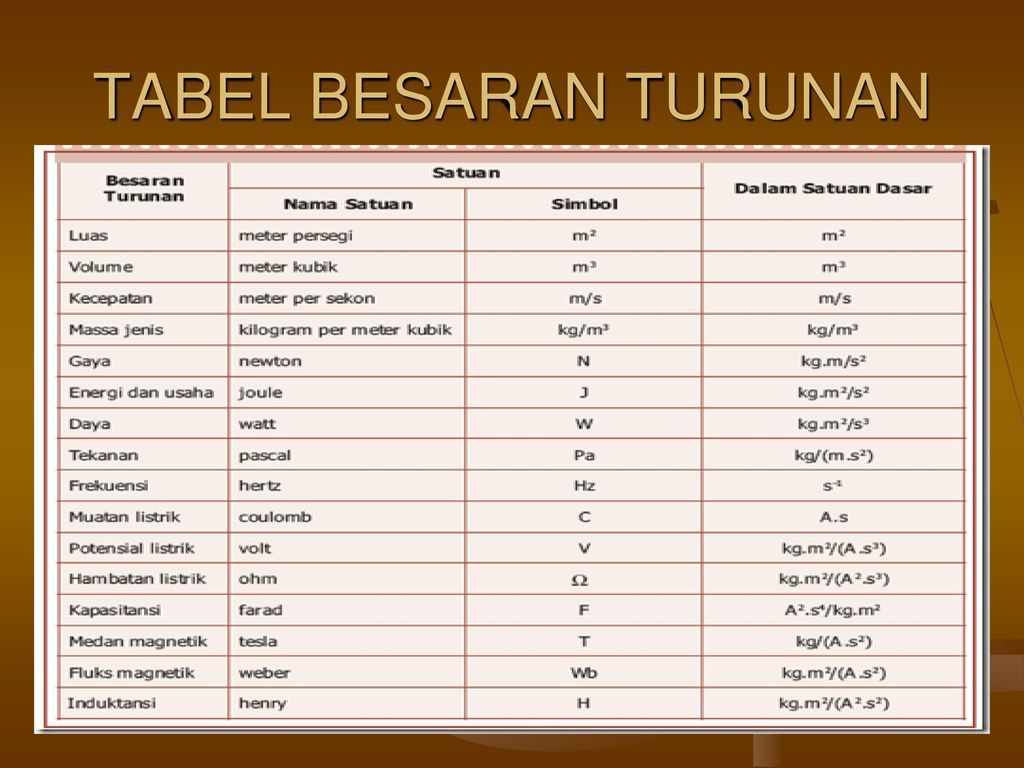
Daftar Contoh Besaran Turunan, Rumus, dan Satuan

Berikut adalah daftar beberapa contoh besaran turunan beserta rumus dan satuannya:

Besaran Turunan	Rumus	Satuan (SI)
Luas	Panjang × Lebar	m² (meter persegi)
Volume	Panjang × Lebar × Tinggi	m³ (meter kubik)
Kecepatan	Jarak / Waktu	m/s (meter per detik)
Percepatan	Perubahan Kecepatan / Waktu	m/s² (meter per detik kuadrat)
Gaya	Massa × Percepatan	N (Newton) atau kg m/s²
Usaha/Energi	Gaya × Jarak	J (Joule) atau kg m²/s²
Tekanan	Gaya / Luas	Pa (Pascal) atau N/m²
Daya	Usaha / Waktu	W (Watt) atau J/s
Massa Jenis	Massa / Volume	kg/m³ (kilogram per meter kubik)

Contoh Soal dan Solusi

Soal: Sebuah mobil bergerak dengan kecepatan konstan 20 m/s selama 15 detik. Berapakah jarak yang ditempuh mobil tersebut?

Solusi:

Rumus yang digunakan: Jarak (s) = Kecepatan (v) × Waktu (t)

Diketahui: v = 20 m/s, t = 15 s

Perhitungan: s = 20 m/s × 15 s = 300 m

Jawaban: Jarak yang ditempuh mobil adalah 300 meter.

Aplikasi dalam Kehidupan Sehari-hari

Contoh Besaran Pokok dan Besaran Turunan Panduan Lengkap dan Mudah Dipahami

Source: grid.id

Konsep besaran pokok dan turunan merupakan fondasi penting dalam memahami dan mengukur fenomena di sekitar kita. Penerapannya sangat luas, mulai dari kegiatan sehari-hari hingga industri teknologi canggih. Pemahaman yang baik terhadap besaran-besaran ini memungkinkan kita untuk menginterpretasikan data, memecahkan masalah, dan membuat keputusan yang lebih tepat.

Contoh Penerapan dalam Kehidupan Sehari-hari

Besaran pokok dan turunan berperan penting dalam berbagai aspek kehidupan. Berikut beberapa contoh nyata:

Memasak: Dalam memasak, kita menggunakan besaran pokok seperti massa (bahan makanan ditimbang), panjang (ukuran bahan), dan waktu (lama memasak). Besaran turunan seperti volume (ukuran wadah) dan kecepatan (memasak dengan api sedang atau besar) juga sangat relevan. Misalnya, resep kue memerlukan pengukuran massa tepung, volume air, dan waktu memanggang.
Transportasi: Perjalanan sehari-hari melibatkan besaran turunan seperti kecepatan (jarak yang ditempuh per waktu) dan percepatan (perubahan kecepatan). Jarak tempuh dan waktu tempuh adalah contoh besaran pokok yang digunakan untuk menghitung besaran turunan.
Olahraga: Dalam olahraga, pengukuran jarak, waktu, dan massa sangat penting. Besaran turunan seperti kecepatan, percepatan, dan energi juga digunakan untuk menganalisis performa atlet.
Medis: Di bidang medis, besaran pokok seperti suhu tubuh, berat badan, dan waktu (durasi pengobatan) digunakan. Besaran turunan seperti laju denyut jantung (detak per menit) dan tekanan darah sangat penting untuk diagnosis dan pemantauan kesehatan.

Penggunaan dalam Bidang Teknologi dan Industri

Besaran pokok dan turunan memiliki peran krusial dalam dunia teknologi dan industri. Penerapannya sangat luas dan mendalam:

Manufaktur: Dalam proses manufaktur, pengukuran presisi sangat penting. Besaran pokok seperti panjang, massa, dan waktu digunakan untuk memastikan kualitas produk. Besaran turunan seperti gaya, tekanan, dan daya digunakan untuk mengontrol proses produksi.
Elektronika: Dalam elektronika, besaran pokok seperti arus listrik, tegangan, dan waktu digunakan. Besaran turunan seperti daya listrik, resistansi, dan frekuensi digunakan untuk merancang dan menganalisis rangkaian elektronik.
Konstruksi: Dalam konstruksi, besaran pokok seperti panjang, luas, dan massa digunakan. Besaran turunan seperti volume, tekanan, dan gaya digunakan untuk merancang dan membangun struktur yang aman dan stabil.
Robotika: Dalam robotika, besaran pokok dan turunan digunakan untuk mengontrol gerakan robot. Besaran pokok seperti panjang, sudut, dan waktu digunakan untuk mengukur posisi dan orientasi robot. Besaran turunan seperti kecepatan, percepatan, dan torsi digunakan untuk mengontrol gerakan robot.

Contoh Pengukuran dalam Aktivitas Sehari-hari

Berikut beberapa contoh pengukuran yang melibatkan besaran pokok dan turunan dalam aktivitas sehari-hari:

Mengukur Tinggi Badan: Menggunakan penggaris atau meteran untuk mengukur tinggi badan adalah contoh penggunaan besaran pokok panjang.
Memantau Kecepatan Kendaraan: Menggunakan speedometer pada kendaraan untuk memantau kecepatan adalah contoh penggunaan besaran turunan kecepatan (jarak/waktu).
Menghitung Luas Ruangan: Mengukur panjang dan lebar ruangan, lalu menghitung luasnya (panjang x lebar) adalah contoh penggunaan besaran pokok panjang dan besaran turunan luas.
Menimbang Bahan Makanan: Menggunakan timbangan untuk mengukur massa bahan makanan adalah contoh penggunaan besaran pokok massa.

Pemecahan Masalah Praktis dengan Besaran Pokok dan Turunan

Pemahaman tentang besaran pokok dan turunan dapat membantu kita memecahkan masalah praktis dalam berbagai situasi:

Perencanaan Perjalanan: Dengan mengetahui jarak tempuh dan kecepatan rata-rata, kita dapat memperkirakan waktu tempuh perjalanan.
Perhitungan Kebutuhan Material: Dalam proyek konstruksi kecil, kita dapat menghitung kebutuhan material berdasarkan ukuran dan volume yang diperlukan.
Analisis Konsumsi Energi: Dengan mengukur daya listrik dan waktu penggunaan, kita dapat menghitung konsumsi energi suatu peralatan.
Perencanaan Keuangan: Dalam perencanaan keuangan, kita dapat menggunakan konsep besaran turunan seperti bunga (perbandingan antara jumlah uang yang diterima dengan jumlah uang yang dipinjamkan) untuk memahami pertumbuhan investasi.

Aplikasi Besaran Turunan dalam Bidang Transportasi

Bidang transportasi sangat bergantung pada besaran turunan untuk operasi dan analisisnya. Mari kita ambil contoh sebuah perjalanan mobil:

Mobil bergerak dari titik A ke titik B. Besaran pokok yang terlibat adalah jarak antara A dan B (misalnya, 100 kilometer) dan waktu tempuh (misalnya, 2 jam). Dari informasi ini, kita dapat menghitung besaran turunan seperti:

Kecepatan Rata-rata: Kecepatan rata-rata dihitung dengan membagi jarak tempuh dengan waktu tempuh (100 km / 2 jam = 50 km/jam). Kecepatan ini penting untuk memperkirakan waktu tiba dan merencanakan perjalanan.
Percepatan: Jika mobil mengalami perubahan kecepatan (misalnya, saat berakselerasi atau mengerem), kita dapat menghitung percepatannya. Percepatan dihitung dengan perubahan kecepatan dibagi waktu. Percepatan membantu kita memahami kinerja mobil dan dampaknya pada konsumsi bahan bakar.
Energi Kinetik: Energi kinetik adalah energi yang dimiliki mobil karena gerakannya. Energi kinetik dihitung berdasarkan massa mobil dan kecepatannya. Pemahaman energi kinetik penting dalam analisis keselamatan dan desain kendaraan.

Analisis ini membantu pengemudi dalam pengambilan keputusan (seperti kecepatan yang aman), perencanaan rute, dan efisiensi bahan bakar. Industri transportasi menggunakan konsep-konsep ini untuk merancang kendaraan, mengelola lalu lintas, dan mengembangkan teknologi transportasi yang lebih efisien dan aman.

Perbandingan dan Perbedaan: Contoh Besaran Pokok Dan Besaran Turunan

Memahami perbedaan mendasar antara besaran pokok dan turunan sangat penting dalam fisika. Perbedaan ini memungkinkan kita untuk mengklasifikasikan dan mengukur fenomena fisik secara akurat. Artikel ini akan membahas perbandingan, perbedaan, serta aplikasi dari kedua jenis besaran tersebut.

Mari kita telaah lebih lanjut mengenai perbedaan dan perbandingan antara besaran pokok dan besaran turunan.

Perbandingan Besaran Pokok dan Turunan dalam Tabel

Perbandingan antara besaran pokok dan turunan dapat dilihat secara jelas melalui tabel berikut, yang mencakup definisi, satuan, dan contoh besaran:

Besaran	Definisi	Satuan (SI)	Contoh
Panjang	Ukuran suatu objek atau jarak antara dua titik.	Meter (m)	Jarak tempuh, tinggi bangunan.
Massa	Jumlah zat yang terkandung dalam suatu benda.	Kilogram (kg)	Massa tubuh, massa benda langit.
Waktu	Interval antara dua kejadian.	Sekon (s)	Durasi perjalanan, periode getaran.
Kuat Arus Listrik	Laju aliran muatan listrik.	Ampere (A)	Arus dalam rangkaian listrik.
Suhu	Derajat panas atau dingin suatu benda.	Kelvin (K)	Suhu ruangan, suhu tubuh.
Jumlah Zat	Jumlah entitas elementer (atom, molekul, ion).	Mole (mol)	Jumlah zat dalam reaksi kimia.
Intensitas Cahaya	Daya pancar cahaya per satuan sudut padat.	Candela (cd)	Kecerahan sumber cahaya.
Luas	Ukuran permukaan suatu objek. Diturunkan dari besaran pokok panjang.	Meter persegi (m²)	Luas lantai, luas permukaan meja.
Volume	Ruang yang ditempati oleh suatu benda. Diturunkan dari besaran pokok panjang.	Meter kubik (m³)	Volume wadah, volume benda padat.
Kecepatan	Laju perubahan posisi suatu benda terhadap waktu. Diturunkan dari besaran pokok panjang dan waktu.	Meter per sekon (m/s)	Kecepatan mobil, kecepatan pesawat.
Percepatan	Laju perubahan kecepatan terhadap waktu. Diturunkan dari besaran pokok panjang dan waktu.	Meter per sekon kuadrat (m/s²)	Percepatan mobil saat akselerasi.
Gaya	Interaksi yang menyebabkan perubahan gerak suatu benda. Diturunkan dari besaran pokok massa, panjang, dan waktu.	Newton (N)	Gaya dorong, gaya tarik.
Energi	Kemampuan untuk melakukan kerja. Diturunkan dari besaran pokok massa, panjang, dan waktu.	Joule (J)	Energi kinetik, energi potensial.
Tekanan	Gaya per satuan luas. Diturunkan dari besaran pokok massa, panjang, dan waktu.	Pascal (Pa)	Tekanan udara, tekanan ban.

Diagram Alir Hubungan Besaran Pokok dan Turunan

Diagram alir berikut menggambarkan hubungan antara besaran pokok dan turunan:

Besaran Pokok (Panjang, Massa, Waktu, Kuat Arus, Suhu, Jumlah Zat, Intensitas Cahaya) -> (Digunakan dalam Rumus) -> Besaran Turunan (Luas, Volume, Kecepatan, Percepatan, Gaya, Energi, Tekanan)

Diagram ini menunjukkan bahwa besaran turunan diturunkan dari kombinasi besaran pokok melalui rumus-rumus fisika.

Contoh Soal Perbedaan Besaran Pokok dan Turunan

Berikut adalah contoh soal untuk menguji pemahaman tentang perbedaan antara besaran pokok dan turunan:

Sebuah mobil bergerak dengan kecepatan konstan 20 m/s. Manakah besaran yang merupakan besaran pokok dan turunan dalam pernyataan ini?

Kecepatan (Turunan)
Waktu (Pokok)
Jarak (Pokok)

Sebuah balok memiliki panjang 5 m, lebar 3 m, dan tinggi 2 m. Hitung volume balok tersebut.

Panjang, lebar, dan tinggi adalah besaran pokok (panjang).
Volume adalah besaran turunan yang dihitung dari perkalian panjang, lebar, dan tinggi (5 m x 3 m x 2 m = 30 m³).

Soal-soal di atas membantu mengidentifikasi besaran pokok dan turunan serta memahami bagaimana besaran turunan dihitung dari besaran pokok.

Perbandingan Besaran Pokok dalam Sistem SI dan Sistem Lainnya

Sistem Satuan Internasional (SI) adalah sistem yang paling umum digunakan dalam ilmu pengetahuan dan teknik. Namun, sistem satuan lain juga ada dan masih digunakan dalam beberapa konteks. Berikut perbandingan singkatnya:

Sistem SI: Menggunakan meter (m) untuk panjang, kilogram (kg) untuk massa, dan sekon (s) untuk waktu.
Sistem CGS (centimeter-gram-second): Menggunakan centimeter (cm) untuk panjang, gram (g) untuk massa, dan sekon (s) untuk waktu. Sistem ini lebih umum digunakan dalam beberapa bidang ilmiah tertentu.
Sistem Imperial (Inggris): Menggunakan inci (in) atau kaki (ft) untuk panjang, pound (lb) untuk massa, dan sekon (s) untuk waktu. Sistem ini masih digunakan di Amerika Serikat.

Perbedaan utama terletak pada satuan yang digunakan, namun konsep dasar besaran pokok tetap sama.

Perbedaan Skalar dan Vektor pada Besaran Turunan

Besaran turunan dapat berupa skalar atau vektor. Perbedaan utama antara keduanya adalah:

Skalar: Hanya memiliki nilai dan satuan. Contoh: Luas, volume, energi.
Vektor: Memiliki nilai, satuan, dan arah. Contoh: Kecepatan, percepatan, gaya.

Contoh:

Kecepatan: Sebuah mobil bergerak dengan kecepatan 60 km/jam ke arah timur. Kecepatan adalah vektor karena memiliki nilai (60 km/jam) dan arah (timur).
Laju: Sebuah mobil bergerak dengan laju 60 km/jam. Laju adalah skalar karena hanya memiliki nilai.

Kesimpulan Akhir

Pemahaman mendalam tentang contoh besaran pokok dan besaran turunan membuka pintu menuju pemahaman yang lebih komprehensif tentang alam semesta. Dengan menguasai konsep dasar ini, siapapun dapat mengaplikasikannya dalam berbagai konteks, mulai dari memecahkan masalah sehari-hari hingga berkontribusi pada kemajuan ilmu pengetahuan dan teknologi. Teruslah belajar dan bereksplorasi, karena dunia fisika menawarkan petualangan tanpa batas bagi mereka yang ingin tahu.